This is the first part of a series (that’s the intention at least 🤣) trying to give an overview, from a broad lens, of what I do in my academic field. It’s machine learning - ML1 - and in this I’ll focus on what it is, while I’ll talk about its applications, research and development in later parts. Keep in mind also that this is the first time I write extensively about what I do in general terms and in a popular format! I’ll explain mainly through examples to try and avoid as possible any formal definitions. I’ll try my best 🙃 and please send feedback, it’ll help!!
ML can help in many fields but the problem to solve often boils down to a prediction. Some pretty famous examples of usage are:
- how will the rates of infection from Covid develop over specific locations in the following weeks and months?
- which advertisements to put in front of a specific user’s eyes to maximize the chance that they will stop scrolling, click and buy?
- how does my iPhone correctly identifies its owner’s face and unlock?
- can we estimate future rates of reoffending for people convicted of crimes?
- how to evaluate workers performance in any given field?2
There are also less popular and yet not less interesting applications, such as:
- how will a community’s population evolve in the coming years, in regards to phenomena like gentrification and segregation?3
- how to help doctors in making more informed diagnostic and treatment decisions?
- how to ensure a prediction is made for ethical reasons?
- how do we isolate, recognize and measure unfairness?
Classical predictive models
There are several ways to try to predict the future. A few common ways are:
- based on human-set rules,
- based on models of reality,
- based on statistical knowledge of historical behavior.
Let’s look at each of them because ML draws concepts from each.
Human-set rules
This is what I refer to as the “classical” way of controlling and predicting behavior in artificial systems. An example would be: if the industrial machine for baking cookies reaches 90 C° on the outside surface, shut it off automatically before it burns. This rule (90 C° external sensor → shut down) is set in this example by a human expert. They know that:
- 90 C° is above the normal temperatures during usage, and
- it’s far enough above the normal to be dangerous to the materials used or to the factory in which the machine is installed or to the humans operating it.
There are fields in which this approach is the gold standard, and probably should be so for a long time (e.g. nuclear power plants control systems). Still, this approach represents some of the roots of ML.
Models of reality
Many engineering design works are first represented in a computer model through programming and design languages. For instance, a highway bridge will be represented in a computer before being built. The same will happen during the design of a space rocket4. The softwares employed allow for artificial perturbation of conditions, like introducing strong winds or earthquakes to check and see what would happen to the bridge as designed.
Statistics and historical behavior
There are several assumptions that we make when trying to infer conclusions from historical behavior using statistics. I won’t talk about all of them here, just one: the concept of a “data generating machine”. The idea is that phenomena are directed by invisible, highly complex mathematical functions that for a set of values of variables (the input of the function) give an outcome to the phenomena (the output of the function).
A (made-up) example
| Variables |
|---|
| number of trains passing on the same tracks today |
| number of passengers for each of those trains |
| detailed weather characteristics |
| experience of train staff including conductors |
| Generates |
|---|
| number of minutes a train will be late at each station |
Once again this example is 100% made up. All I’m trying to picture is the hypothesis, made in statistics, of the existence of a specific relationship between variables (the characteristics of the causes of the phenomenon) and the outcome of the phenomenon itself (in this case, how many minutes the train will be late). The idea of a data generating machine is that there exists a maths function that formalizes this relationship and assigns unique values of the outcome to each set of inputs.
Much of the predictive statistical modeling work is to try and figure out this function5 as accurately as possible. There are many possible techniques. We’re getting closer to machine learning.
Inference of an approximate function
A regression is one of these statistical predictive techniques and is used to extract this function from a set of data. The data consists of sets of variable values and outcomes. We call the variables “features” and the outcome “class” or “dependent/target variable”6.
Another example
Let’s suppose that the phenomenon in question is the causal connection between the number of years of formal education that a person had and their current monthly revenue. We’re hypothesizing that the first determines the second. These might be the data we have (made up, but realistic7):
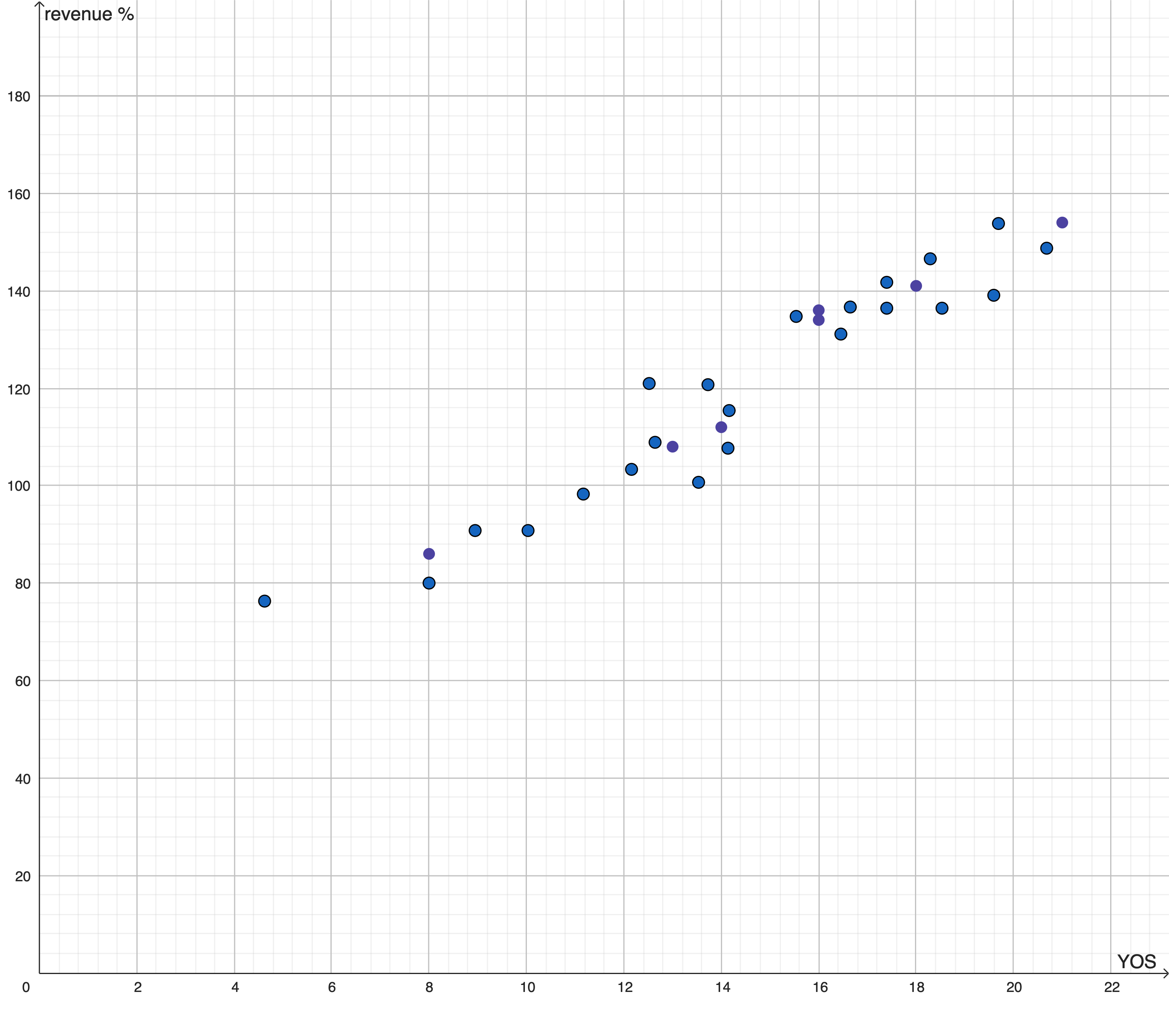
The process of applying regression might extract this function, in pink:
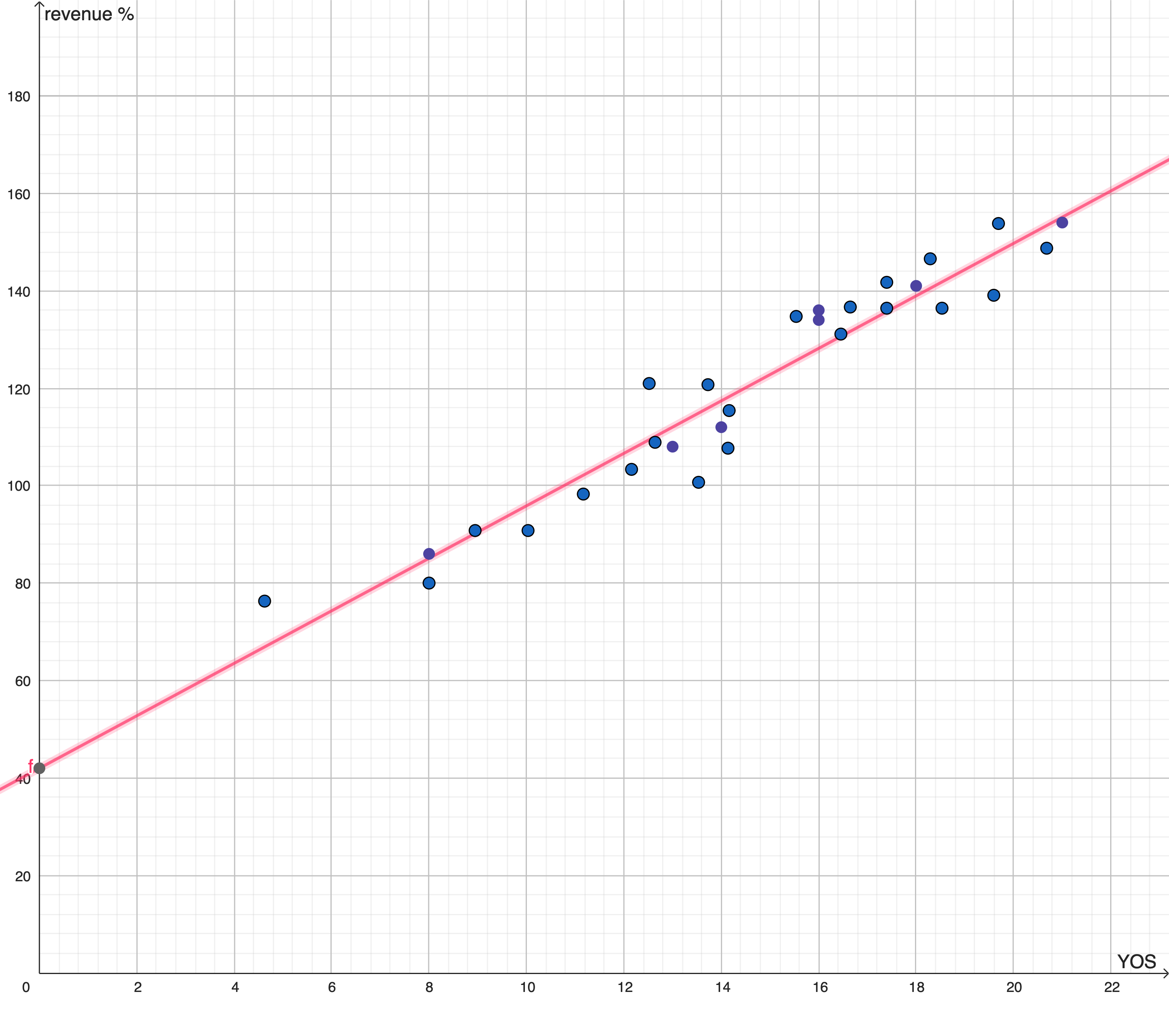
This function does not provide, for each value of the feature, values of the phenomenon that exactly mirror the input data. Instead, for each value of X it provides the value lying on the segment drawn. It’s just the best function that can be inferred from the data given the algorithm chosen by the operator; in this case, the algorithm is a “linear regression with 1 regressor and the OLS optimization function”.
A deep dive on linear regression is here in a 30 minute really well-made video by a fantastic YouTube channel, StatQuest.
Machine learning predictive models
All of these three concepts play a role in ML. Applying ML to a predictive problem means all of the following:
- Modeling reality, that is creating a model of reality - although the model is automatically inferred instead of being intelligently designed by the operator;
- A model that is (often) based on rules - although:
- the rules might be so complex they don’t make sense to the human, or
- the rules might look like different types of rules than what you would expect8, or, finally,
- the rules might not look like rules at all.
- A model whose behavior and/or rules are (often) inferred from statistical, historical data9.
The purpose of creating this model is to try and predict the behavior of our phenomenon of interest based on the data (circumstances and outcomes, a.k.a. features and target variables) that same phenomenon generated in the past.
Next articles…
I’m thinking some interesting points to touch in the next parts are:
- what is the role of a human operator in ML?
- What are objective functions?
- What are some of the most crucial issues with this?
- What are interesting research directions right now?
- How does ML influence society?
Do let me know some points you’d like to read about, as well as any questions!! I’m particularly interested on how accessible this text was for non-experts. Looking forward for your feedback!
Further reading
- An MIT article, a bit more in depth on specific ML categories and on the relationship between private business and ML.
-
Part of the field that is sometimes called artificial intelligence, but I don’t like that denomination. ↩︎
-
In trying to paint a complete picture, I’ll mention all applications, not only the ethical ones. These last two examples, in particular, have come to the attention of the American press for their callousness. ↩︎
-
For those interested, an article announcing the publication of an interesting scientific paper regarding this very issue. ↩︎
-
In fact, there’s even a simulation game to build space vehicles. It’s Kerbal Space Program. I got it and tried it, but never got the hang of it, I’m really bad at building things. Same reason why I never got the hang of Minecraft. 😝 ↩︎
-
A function that, again, is hypothetical and might not exist. As an example, one might make the hypothesis that at the core of weather is a maths function. It’s a conjecture that we might never be able to verify, because there is no theoretical limit to the possible complexity of a function. We can exclude many functions from being candidates of generating a phenomenon, but it’s hard to prove that we can exclude all functions. ↩︎
-
One possible form of this function might look like $y = \beta _0 + \beta _1 x_1 + \beta _2 x_2$. This is a linear regression with two features $x_1$ and $x_2$ and a residual $\beta _0$. In regression the features can also be called independent variables or regressors. ↩︎
-
Source: OECD’s Education and earnings, Australia, 2020, 25-64 years of age. ↩︎
-
Example, based on geometry, on unusual measures of dissimilarity, or on proxy representations of reality. ↩︎
-
There are two ways to do statistical inference: one is inferring future behavior of the objects you are investigating, and is based on historical data of those same objects. The other is inferring behavior of different objects than those you have data on, but still belonging to the same population. An example is inferring the behavior of all voters when you have data (surveys) on just a smaller group of voters. In this article I spoke on the first of these two approaches, but much of the same concepts apply to the second approach. ↩︎